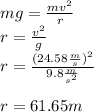Question

An automobile moves at a constant speed over the crest of a hill traveling at a speed of 88.5 km/h. At the top of the hill, a package on a seat in the rear of the car barely remains in contact with the seat. What is the radius of curvature (m) of the hill?

Answer 1

`r=61.65m`

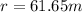
Step-by-step explanation:

Since the package remains in contact with the car's seat, the package's speed is equal to the car's speed. At the top on the mountain the package's centripetal force must be equal to its weight:

`mg=F_c`

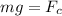
The centripetal force is defined as:

`F_c=ma_c=(mv^2)/(r)`

Here v is the linear speed of the object and r is the radius of curvature. We need to convert the linear speed to
`(m)/(s)`:

`88.5(km)/(h)*(1000m)/(1km)*(1h)/(3600s)=24.58(m)/(s)`

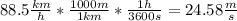
Now, we calculate r:

`mg=(mv^2)/(r)\\r=(v^2)/(g)\\r=((24.58(m)/(s))^2)/(9.8(m)/(s^2))\\\\r=61.65m`