Question

Trevor decides to start saving money for a new car. He knows he can invest money into an account which will earn 6.8% APR, compounded weekly, and would like to have saved $12,000 after 4 years. How much money will he need to invest into the account now so that he has $12,000 after 4 years.

Answer 1

PV=$9,143.88

Explanation:

Compound Interest

When a principal amount (also called present value PV) is saved at some rate of interest r for some time t, the future value FV that includes the original investment plus the interests is computed as

`FV=PV\left(1+r\right)^t`

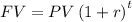
If the investment is compounded other than annually, then r and t must be scaled to the proper time units.

If we already know the future value, then the present value is computed by solving the above equation

`PV=FV\left(1+r\right)^(-t)`

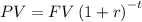
The Annual Percentage Rate (APR) is 6.8% compounded weekly, so the value of r is (assuming 52 weeks per year)

`\displaystyle r=(6.8)/(100* 52)=0.00131`

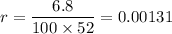
And the time is computed in weeks

t=4*52=208

The present value of the investment Trevor needs to save now is

`PV=12,000\left(1+0.00131\right)^(-208)`

`\boxed{PV=\$9,143.88}`

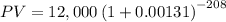
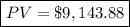
Trevor will need to invest $9,143.88 into the account to have $12,000 after 4 years