The length of the rug is 4 ft.
The width of the rug is 2.5 ft.
Step-by-step explanation:
The area of the rug is 10 ft.
The length of the rug be l.
Let us convert the inches to feet.
Thus,
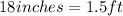
Thus, the length of the rug is
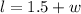
Let the width of the rug be w.
Substituting these values in the formula of area of the rectangle, we get,
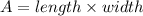
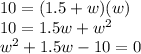
Solving the expression using the quadratic formula,
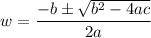
Substituting the values, we have,
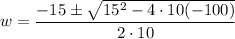
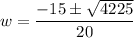
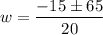
Thus,
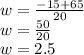 and
and
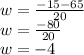
Since, the value of w cannot be negative, the value of w is 2.5ft
Thus, the width of the rug is 2.5ft
Substituting
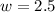 in
in
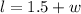 , we get,
, we get,
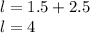
Thus, the length of the rug is 4 ft.