Question

Determine the equation of the line that is perpendicular to the lines r​(t) equalsleft angle6​t,1 plus3 ​t,4tright angle and R​(s)equalsleft angle 2 plus​s,negative 8 plus 3​s,negative 12 plus 4 sright angle and passes through the point of intersection of the lines r and​ R, where tau equals 0 corresponds to the point of intersection.

Answer 1

`\vec r(t)=\langle6t,1+3t,4t\rangle`

`\vec R(s)=\langle2+s,-8+3s,-12+4s\rangle`

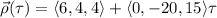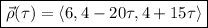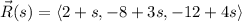
Take the derivatives of each to get the tangent vectors:

`(\mathrm d\vec r(t))/(\mathrm dt)=\langle6,3,4\rangle`

`(\mathrm d\vec R(s))/(\mathrm ds)=\langle1,3,4\rangle`

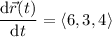
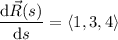
Take the cross product of the tangent vectors to get a vector that is normal to both lines:

`\langle6,3,4\rangle*\langle1,3,4\rangle=\langle0,-20,15\rangle`

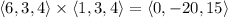
The two given lines intersect when
`\vec r(t)=\vec R(s)`:

`\langle6t,1+3t,4t\rangle=\langle2+s,-8+3s,-12+4s\rangle\implies t=1,s=4`

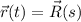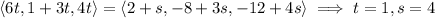
that is, at the point (6, 4, 4).

The line perpendicular to both of the given lines through the origin is obtained by scaling the normal vector found earlier by
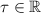`\tau\in\Bbb R`; translate this line by adding the vector
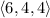`\langle6,4,4\rangle` to get the line we want,

`\vec\rho(\tau)=\langle6,4,4\rangle+\langle0,-20,15\rangle\tau`

`\boxed{\vec\rho(\tau)=\langle6,4-20\tau,4+15\tau\rangle}`