Question

A roller coaster of mass 3000.0 kg starts from rest at Point A, which is 33 meters above the bottom of the coaster and proceeds to point C, which is 15 m above the bottom of the coaster. a) What is its speed at C? b) Recall that the formula for critical velocity is: If the radius of the loop is 5.0 m, will the roller coaster have enough kinetic energy at the top of the loop to satisfy the critical velocity criteria?

Answer 1

Complete answer

A roller coaster of mass 3000.0 kg starts from rest at Point A, which is 33 meters above the bottom of the coaster and proceeds to point C, which is 15 m above the bottom of the coaster. a) What is its speed at C? b) Recall that the formula for critical velocity is:
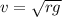`v=√(rg)` If the radius of the loop is 5.0 m, will the roller coaster have enough kinetic energy at the top of the loop to satisfy the critical velocity criteria?

Answer:

The roller coaster has enough kinetic energy.

Step-by-step explanation:

Assuming there are not dissipative forces between the cart and the rails of the roller coaster, we can use conservation of energy between A and C:

`E_A=E_B=K_A+U_A=K_C+U_C` (1)

with K kinetic energy and U potential gravitational energy. Kinetic energy is defined as:

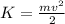`K=(mv^2)/(2)` (2)

with v the velocity and m the mass. If we choose zero of potential energy at the bottom of the roller coaster, the gravitational potential energy is:

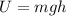`U=mgh` (3)

with gravitational acceleration and h the height of the cart. Using (2) and (3) on (1):

`(mv_A^2)/(2)+mgh_A=(mv_C^2)/(2)+mgh_C`

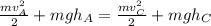
Solving for VB and knowing that velocity on A is zero because the cart starts from rest:

`v_C=\sqrt{((2)/(m))(mgh_A-mgh_C)}=√(2*9.81(33-15))=18.78(m)/(s)`

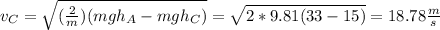
b) Critical velocity is
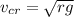`v_(cr)=√(rg)` in our case:

`v_(cr)=√(5*9.81)=7.00 (m)/(s)`

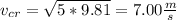
So, the critical kinetic energy is:

`K_cr=((3000.0)(7.0)^2)/(2)=73500J`

Now we should check that the value of kinetic energy at 5m is more or equal to that value. We can use the equation used on a)

`mgh_A=K_5+mgh_5`

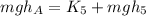
solving for K5:

`K_5=mg(h_A-h_5)=(3000.0)(9.81)(33-5)=824040 J`

It is bigger than Kc, so the roller coaster has enough kinetic energy.