Question

What is x given triangleABC ~triangleDBE?

Answer 1

x = 37.5 (or)
`(75)/(2)`

Solution:

Given
`\triangle A B C \sim \triangle D B E`.

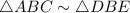Let us take BE = x and BC = 25 + x.

To determine the value of x:

If two triangles are similar then the corresponding angles are congruent and the corresponding sides are in proportion.

`$(AC)/(DE)=(B C)/(B E)`

`$(50)/(30) =(25+x)/(x)`

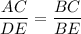
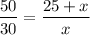
Do cross multiplication, we get

`50x=30(25+x)`

`50x=750+30x`

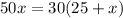
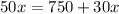
Subtract 30x from both sides of the equation.

`20 x=750`

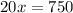
Divide by 20 on both sides of the equation, we get

x = 37.5 (or)
`(75)/(2)`

Hence the value of x is 37.5 or
`(75)/(2)`.