Question

Two identical parallel plate capacitors are given the same charge Q, after which they are disconnected from the battery. After C2 has been charged and disconnected, it is filled with a dielectric. How are the potential energies of each capacitor related? U1 = U2 U1 < U2 U1 > U2

Answer 1

U₁ > U₂

Step-by-step explanation:

By definition, the capacitance of a capacitor, can be expressed as follows:

`C = (Q)/(V) (1)`,

where Q is the charge on one of the terminals of the capacitor, and V, the potential difference between them.

If the capacitors are of the parallel plate type, applying Gauss ' law to a gaussian surface defined as a pill box parallel to the surface of one of the plates (half outside the plate, half inside it) , the capacitance can be expressed as follows:

`C = (\epsilon*A)/(d) (2)`

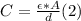
where ε is the dielectric constant of the material that fills the space between plates, A is the area of one of the plates (assuming a constant surface charge density) and d is the distance between the plates.

If both capacitors have the same charge Q, as they are identical, the potential difference V must be the same for both capacitors also.

So, the electric potential energy, for both capacitors, can be written as follows:

`Ue = U1 = U2 = (1)/(2)*(Q^(2))/(C)`

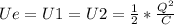
Now, if after being charged and disconnected (which means that the charge must keep the same), C₂ is filled with a dielectric, looking to the equation (2), we can see that the value of the capacitance, will increase, proportionally to the value of the dielectric constant of the dielectric.

If we analyze the expression (3) for the electric potential energy stored in the capacitor, as Q₂ = Q₁, and being C₂ = ε*C₁, this means that the electric potential energy U₂ must be lower than U₁, in the same factor ε, as follows:

`U2 = (1)/(2)*(Q^(2))/(C2) = (1)/(2)*(Q^(2))/(\epsilon*C1) = (1)/(\epsilon) *( (1)/(2)*(Q^(2))/(C1)) = (1)/(\epsilon) * U1`

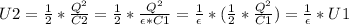
⇒ U₁ > U₂