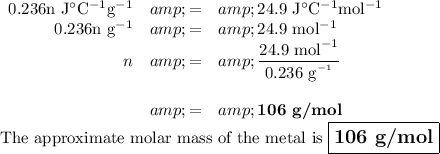Question

a 58.215 g sample of a pure metal is brought to 99.0c and added o 41.202 g of water at 21.5c in a calorimeter. if the metal and water arrive at a final, equal temerature of 27.2c find a) the specific heat of the metal, and b) the approximate molar mass of yhe metal

Answer 1

The answer to your question is a) C = 0.056 cal/g°C b) 107.8 g/mol

Step-by-step explanation:

I included a picture of the problem because it says that it has inappropriate words or links

Answer 2

`\boxed{\text{(a) 0.236 J$^(\circ)$C$^(-1)$g$^(-1)$; (b) 106 g/mol}}`

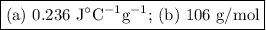
Step-by-step explanation:

a) Specific heat capacity of the metal

The guiding principle in calorimetry is the Law of Conservation of Energy: the sum of all the energy transfers must add up to zero. That is,

q₁ + q₂ + … = 0

The formula for the heat q gained or lost by a substance is

q = mCΔT

where

m = the mass of the substance.

C = its specific heat capacity.

ΔT = the change in temperature.

In this problem, there are two heat transfers: the heat lost by the metal and the heat gained by the water.

m₁C₁ΔT₁ + m₂C₂ΔT₂ = 0

Data:

m₁ = 58.215 g; T₁ = 99.0 °C; T₂ = 27.2 °C

m₂ = 41.202 g; T₁ = 21.5 °C; T₂ = 27.2 °C

Calculations:

ΔT₁ = 27.2 - 99.0 = -71.8 °C

ΔT₂ = 27.2 - 21.5 = 5.7 °C

`\begin{array}{rcl}\text{heat lost by metal} + \text{heat gained by water} & = & 0\\m_(1)C_(1)\Delta T_(1) + m_(2)C_(2)\Delta T_(2)& = & 0\\\text{58.215 g $*$ C$_(1) *$ (-71.8 $^(\circ)\text{C}$)} + \text{41.202 g} * 4.184 \text{ J$^(\circ)$C$^(-1)$g$^(-1)$} * 5.75^(\circ)\text{C} & = & 0\\-4180C_(1)\text{ g}^(\circ)\text{C} + 987 \text{ J} & = & 0\\\end{array}\\`

`\begin{array}{rcl}-4180C_(1)\text{ g}^(\circ)\text{C}& = & -987 \text{ J}\\C_(1)& = & \frac{-987 \text{ J}}{-4180 \text{ g}^(\circ)\text{C}}\\\\& = & \textbf{0.236 J$^(\circ)$C$^(-1)$g$^(-1)$} \\\end{array}\\\text{The specific heat capacity of the metal is $\boxed{\textbf{0.236 J$^(\circ)$C$^(-1)$g$^(-1)$}}$}`

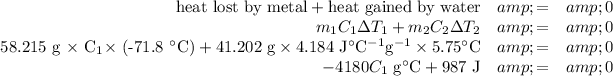
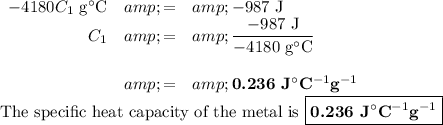
b) Approximate molar mass of the metal

We could look up the metal that has the calculated specific heat capacity, but that would give the exact molar mass.

They asked for the approximate value, do they are probably expecting you to do something else.

Per the Law of Dulong and Petit, the molar specific heat capacity of a metal should be about 24.9 J·°C⁻¹mol⁻¹

`\begin{array}{rcl}\text{0.236n J$^(\circ)$C$^(-1)$g$^(-1)$} & = & \text{24.9 J$^(\circ)$C$^(-1)$mol$^(-1)$}\\\text{0.236n g$^(-1)$} & = & \text{24.9 mol$^(-1)$}\\n & = & \frac{24.9\text{ mol}^(-1)}{0.236\text{ g}^{^(-1)}}\\\\&= &\textbf{106 g/mol}\\\end{array}\\\text{The approximate molar mass of the metal is $\large \boxed{\textbf{106 g/mol}}$}`