Question

Suppose that the number of drivers who travel between a particular origin and destination during a designated time period has a Poisson distribution with parameter?=20. What is the probability that the number of drivers will

A.) Be at most 10?

B.) Exceed 20?

C.) Be Between 10 and 20, inclusive? Be strictly between 10 and 20?

D.) Be within 2 standard deviations of the mean value?

Answer 1

(A) The probability that the number of drivers will be at most 10 is 0.011.

(B) The probability that the number of drivers will exceed 20 is 0.441.

(C) The probability that the number of drivers will be between 10 and 20 (inclusive) is 0.5483 and excluding 10 and 20 is 0.459.

(D) The probability that the number of drivers will within 2 standard deviations of the mean is 0.9549.

Explanation:

Let X = number of drivers who travel between a particular origin and destination during a designated time period.

The random variable
`X\sim Poisson(\lambda=20)`

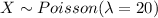
The probability function of a Poisson distribution is:

`\\ P(X=x)=(e^(-\lambda)\lambda^(x))/(x!);\ x=0, 1, 2, ...`

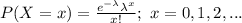
(A)

Compute the probability that the number of drivers will be at most 10 as follows:

P (X ≤ 10) = P (X = 0) + P (X = 1) + P (X = 2) ... + P (X = 10)

`=(e^(-20)20^(0))/(0!)+(e^(-20)20^(1))/(1!)+(e^(-20)20^(2))/(2!)...+(e^(-20)20^(9))/(9!)+(e^(-20)20^(10))/(10!)\\=0.00+0.00+0.00...+0.00291+0.00582\\=0.01081\\\approx0.011`

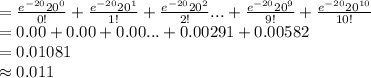
Thus, the probability that the number of drivers will be at most 10 is 0.011.

(B)

Compute the probability that the number of drivers will exceed 20 as follows:

P (X > 20) = 1 - P (X ≤ 20)

= 1 - [P (X = 0) + P (X = 1) + P (X = 2) ... + P (X = 19) + P (X = 20)]

`=1-[(e^(-20)20^(0))/(0!)+(e^(-20)20^(1))/(1!)+(e^(-20)20^(2))/(2!)...+(e^(-20)20^(19))/(9!)+(e^(-20)20^(20))/(20!)]\\=1-[0.00+0.00+0.00...+0.0884+0.08884]\\=1-0.55909\\=0.44091\\\approx0.441`

Thus, the probability that the number of drivers will exceed 20 is 0.441.

(C)

Compute the probability that the number of drivers will be between 10 and 20 (inclusive) as follows:

P (10 ≤ X ≤ 20) = P (X ≤ 20) - P (X ≤ 10)

`=0.5591-0.011\\=0.5483`

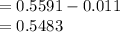
Compute the probability that the number of drivers will be exactly between 10 and 20 as follows:

P (10 < X < 20) = P (X = 11) + P (X = 12) + ... + P (X = 19)

`=(e^(-20)20^(11))/(11!)+(e^(-20)20^(12))/(12!)+(e^(-20)20^(13))/(13!)...+(e^(-20)20^(19))/(19!)\\=0.01058+0.01763+0.02712...+0.08884\\=0.45945\\\approx0.459`

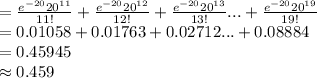
Thus, the probability that the number of drivers will be between 10 and 20 (inclusive) is 0.5483 and excluding 10 and 20 is 0.459.

(D)

The mean of a Poisson distribution is,
`\mu=\lambda=20`

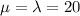
The standard deviation of a Poisson distribution is:

`\sigma=√(\lambda) =√(20)=4.47`

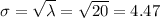
Compute the probability that the number of drivers will within 2 standard deviations of the mean as follows:

`P(\mu-2\sigma<X<\mu+2\sigma)=P(20-(2*4.47)<X<20+(2*4.47))\\=P(11.06<X<28.94)\\\approx P(11<x<29)\\=P(X<29)-P(X<11)\\= 0.9657-0.0108\\=0.9549`

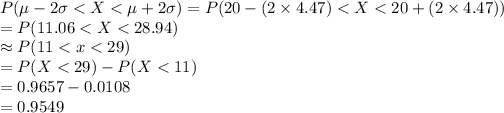
Thus, the probability that the number of drivers will within 2 standard deviations of the mean is 0.9549.