Question

High blood cholesterol increases your risk of heart attack and stroke. Cholesterol levels in young women are approximately Normal with mean 189 mg/dl and standard deviation 40 mg/dl. About 34% of women will have levels between _______________.

Answer 1

• About 34% of women will have levels between:

171 mg/dl and 207 mg/dl

Step-by-step explanation:

You might find several intervals of cholesterol levels that contain about 34% of the women.

The easiest way is to find a symmetric interval. This is, with the same number of women below and above the mean.

Then, if 34% of the women are within the interval, 100% - 34% = 66% are out of the interval.

For a symmetric interval, half of 66% would be above the median and half-below the median.

Thus, 33% above and 33% below the median.

Now, you can look up the Z-score in a standard normal distribution table.

There are two types of standard distribution tables: tables that show values that represent the AREA to the LEFT of the Z-score, and tables that show values that represent the AREA to the RIGHT of the Z-score.

Using the second, find the Z-score for a probability of 33%, i.e. 0.33, it is Z-score = 0.44.

That means that the interval must be - 0.44 < Z-score < 0.44

Now that you have the Z-score you can find the cholesterol levels:

For the upper level:

`Z-score=\frac{\text{cholesterol level-mean}}{\text{standard deviation}}`

`Z-score=(x-189)/(40)`

`0.44=(x-189)/(40)`

`x=0.44* 40+189=206.6`

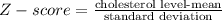
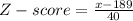
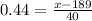
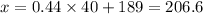
For the lower level:

`-0.44=(x-189)/(40)`

`x=-0.44* 40+189=171.4`

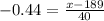
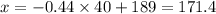
Rounding to whole numbers the interval would be between 171 mg/dl and 207 mg/dl.