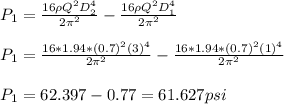Question

Water flows steadily through a horizontal nozzle, discharging to the atmosphere. At the nozzle inlet the diameter is D1; at the nozzle outlet the diameter is D2. i) Derive an expression for the minimum gage pressure required at the nozzle inlet to produce a given flow rate, Q. Evaluate the inlet gage pressure if D1

Answer 1

Complete question:

Water flows steadily through a horizontal nozzle, discharging to the atmosphere. At the nozzle inlet, the diameter is D1, at the nozzle outlet the diameter is D2. i) Derive an expression for the minimum gauge pressure required at the inlet to produce a given volume flow rate Q.

ii) Evaluate the inlet gauge pressure if D1=3.0in, D2=1.0in and the desired flow rate is 0.7 ft³/sec. Assume density of water is 1.94 slug/ft³.

Answer:

Part (i)
`P_1 = (16\rho Q^2D_2^4)/(2\pi^2 ) - (16\rho Q^2D_1^4)/(2\pi^2 )`

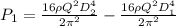
part (ii) the inlet gauge pressure is 61.627 Psi

Step-by-step explanation:

Applying Bernoulli's equation

`P_1 + \rho gZ_1 +(\rho U_1^2)/(2) = P_2 + \rho gZ_2 +(\rho U_(2)^2)/(2) +P_L`

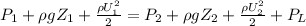
Where;

P₁ is the gauge pressure at the inlet nozzle

Z₁ is the vertical height above ground

U₁ is the inlet velocity

P₂ is the gauge pressure at the outlet nozzle

Z₂ is the vertical height above ground

U₂ is the outlet velocity

ρ is the density of water

PL is the pressure of water at the outlet nozzle

Assumptions

for a horizontal flow that discharges to the atmosphere;

• the potential is zero and there is no loss of energy due to height.
• the gauge pressure at the outlet nozzle is zero

The equation reduces to;

`P_1 +(\rho U_1^2)/(2) = (\rho U_(2)^2)/(2)`

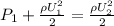
Part(i)

And minimum gauge pressure at the inlet nozzles becomes;

`P_1 = (\rho U_(2)^2)/(2) -(\rho U_1^2)/(2)`

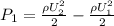
Substituting for flow rate Q; from continuity equation

U = Q/A

`A = (\pi D^2)/(4)`

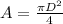
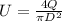`U =(4Q)/(\pi D^2)`, Substitute this for U in the minimum gauge pressure equation above.

`P_1 = (\rho ((4Q)/(\pi ) D^2 _(2))^2)/(2) -(\rho ((4Q)/(\pi ) D^2 _(1))^2)/(2)\\\\`

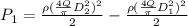
The equation for the minimum gauge pressure required at the nozzle inlet to produce a given flow rate, Q, becomes;

`P_1 = (16\rho Q^2D_2^4)/(2\pi^2 ) - (16\rho Q^2D_1^4)/(2\pi^2 )`

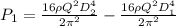
Part (ii)

given;

inlet diameter D₁ = 3.0 in

outlet diameter D₂ = 1.0 in

water flow rate Q = 0.7 ft³/sec

density of water ρ = 1.94 slug/ft³

Substitute these values in the equation above and evaluate P₁

`P_1 = (16\rho Q^2D_2^4)/(2\pi^2 ) - (16\rho Q^2D_1^4)/(2\pi^2 )\\\\P_1 = (16*1.94* (0.7)^2(3)^4)/(2\pi^2 ) - (16*1.94* (0.7)^2(1)^4)/(2\pi^2 )\\\\P_1 =62.397 - 0.77 = 61.627 psi`