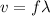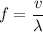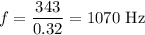Question

A 40-cmcm-long tube has a 40-cmcm-long insert that can be pulled in and out. A vibrating tuning fork is held next to the tube. As the insert is slowly pulled out, the sound from the tuning fork creates standing waves in the tube when the total length LL is 42.5 cmcm , 58.5 cmcm

What is the frequency of the tuning fork? Assume velocity of sound = 343 m/s

Answer 1

1070 Hz

Step-by-step explanation:

First, I should point out there might be a typo in the question or the question has inconsistent values. If the tube is 40 cm long, standing waves cannot be produced at 42.5 cm and 58.5 cm lengths. I assume the length is more than the value in the question then. Under this assumption, we proceed as below:

The insert in the tube creates a closed pipe with one end open and the other closed. For a closed pipe, the difference between successive resonances is a half wavelength
`(\lambda)/(2)`.

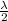Hence, we have

`(\lambda)/(2)=58.5-42.5=16 \text{ cm}`

`\lambda=32\text{ cm}=0.32 \text{ m}`.

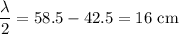
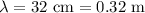The speed of a wave is the product of its wavelength and its frequency.

`v=f\lambda`

`f=(v)/(\lambda)`

`f=(343)/(0.32)=1070 \text{ Hz}`