Answer: The enthalpy of formation of HCN(g) is 135.1 kJ/mol
Step-by-step explanation:
Enthalpy change is defined as the difference in enthalpies of all the product and the reactants each multiplied with their respective number of moles.
The equation used to calculate enthalpy change is of a reaction is:
![\Delta H^o_(rxn)=\sum [n* \Delta H_f_((product))]-\sum [n* \Delta H_f_((reactant))]](https://img.qammunity.org/2021/formulas/chemistry/high-school/d42uy6x9fukypqy4uarr52v887yviorkhi.png)
For the given chemical reaction:
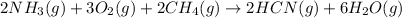
The equation for the enthalpy change of the above reaction is:
![\Delta H_(rxn)=[(2* \Delta H_f_((HCN(g))))+(6* \Delta H_f_((H_2O(g))))]-[(2* \Delta H_f_((NH_3(g))))+(3* \Delta H_f_((O_2(g))))+(2* \Delta H_f_((CH_4(g))))]](https://img.qammunity.org/2021/formulas/chemistry/high-school/7iz7d9o5n73950fu2jnry6hqfjefugh5uj.png)
We are given:
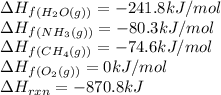
Putting values in above equation, we get:
![-870.8=[(2* \Delta H_f_((HCN(g))))+(6* (-241.8))]-[(2* (-80.3))+(3* (0))+(2* (-74.6))]\\\\\Delta H_f_((HCN(g)))=135.1kJ/mol](https://img.qammunity.org/2021/formulas/chemistry/high-school/tyamc69sp0jn95y220hff8n6qien6m0tk5.png)
Hence, the enthalpy of formation of HCN(g) is 135.1 kJ/mol