Question

In a start-up company which has 20 computers, some of the computers are infected with virus. The probability that a computer is infected with the virus is 0.4, independently of other computers. A technician tests the computers, one after another, to see if they are infected.1. What is the probability that she has to test at least 5 computers to find the first (if any) defective one?2. Find the probability that on this day at least 5 computers are infected.

Answer 1

(1) The probability that the technician tests at least 5 computers before the 1st defective computer is 0.078.

(2) The probability at least 5 computers are infected is 0.949.

Explanation:

The probability that a computer is defective is, p = 0.40.

(1)

Let X = number of computers to be tested before the 1st defect is found.

Then the random variable
`X\sim Geo(p)`.

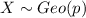The probability function of a Geometric distribution for k failures before the 1st success is:

`P (X = k)=(1-p)^(k)p;\ k=0, 1, 2, 3,...`

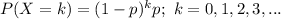
Compute the probability that the technician tests at least 5 computers before the 1st defective computer is found as follows:

P (X ≥ 5) = 1 - P (X < 5)

= 1 - [P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3) + P (X = 4)]

`=1 -[(1-0.40)^(0)0.40+(1-0.40)^(1)0.40+(1-0.40)^(2)0.40\\+(1-0.40)^(3)0.40+(1-0.40)^(4)0.40]\\=1-[0.40+0.24+0.144+0.0864+0.05184]\\=0.07776\\\approx0.078`

Thus, the probability that the technician tests at least 5 computers before the 1st defective computer is 0.078.

(2)

Let Y = number of computers infected.

The number of computers in the company is, n = 20.

Then the random variable
`Y\sim Bin(20,0.40)`.

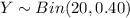The probability function of a binomial distribution is:

`P(Y=y)={n\choose y}p^(y)(1-p)^(n-y);\ y=0,1,2,...`

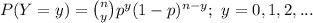
Compute the probability at least 5 computers are infected as follows:

P (Y ≥ 5) = 1 - P (Y < 5)

= 1 - [P (Y = 0) + P (Y = 1) + P (Y = 2) + P (Y = 3) + P (Y = 4)]
`=1-[{20\choose 0}(0.40)^(0)(1-0.40)^(20-0)+{20\choose 1}(0.40)^(1)(1-0.40)^(20-1)\\+{20\choose 2}(0.40)^(2)(1-0.40)^(20-2)+{20\choose 3}(0.40)^(3)(1-0.40)^(20-3)\\+{20\choose 4}(0.40)^(4)(1-0.40)^(20-4)]\\=1-[0.00004+0.00049+0.00309+0.01235+0.03499]\\=1-0.05096\\=0.94904`

Thus, the probability at least 5 computers are infected is 0.949.