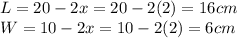Question

An open box is made from a 20 cm x 3 cm piece of tin by cutting a square from each corner and folding up the edges. The area of the resulting base is 96 cm². What is the length of the sides of the squares.

Answer 1

Length of the final sides: 6 cm and 16 cm

Explanation:

The lengths of the sides of the original box are

`L=20 cm\\W=10 cm`

Later, a piece of tin is cut out from each corner; the piece cut out has the shape of the square: we can call the length of its generic side x. Therefore, the dimensions of the box will now be:

`L'=L-2x\\W'=W-2x`

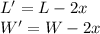
We also know that the area is

`A=96 cm^2`

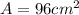
And the area can be written as product of length and width, therefore:

`A=L'W'`

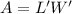
So we find:

`A=(L-2x)(W-2x)\\96=(20-2x)(10-2x)`

Solving for x,

`96=200-20x-40x+4x^2\\4x^2-60x+104=0\\\\x^2-15x-26=0`

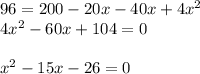
Which has two solutions:

x = 13 cm (this is larger than the initial length of the width, therefore we discard it)

x = 2 cm

So, the length of the new sides are

`L=20-2x=20-2(2)=16 cm\\W=10-2x=10-2(2)=6 cm`