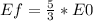Answer:
5/3
Step-by-step explanation:
Assuming that the charge is evenly distributed on the surface of the sphere, by symmetry, at a same distance of the sphere, the electric field must be radial, and of the same magnitude.
So, if we define a spherical gaussian surface with radius equal to 2*R, we can find the total flux as follows:
Flux = E*A = E*4*π*(2*R)² (1)
Now, Gauss' Law states that the flux we have just found must be equal to the charge enclosed, divided by the permitivitty of free space, ε₀:
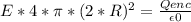
Rearranging terms, and solving for E, we find the following expression:
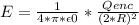
As it can be seen, the electric field, at a distance 2R from the center, is just the same that it would produce a point charge with the same value of Qenc, located in the center of the sphere.
If we keep the same distance, and increase the charge value to 5/3 Q, we can easily see that the electric field (which is linear with the charge) will increase in the same factor, i.e. , 5/3.
⇒