Period is 1
Solution:
Given that,
For the simple harmonic motion equation:
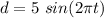
To find: Period
Use the following form to find the period
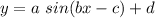
Where,
a is the amplitude
c is phase shift
d is vertical shift
The period is given as:

On comparing,
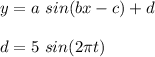
Thus on comparing we get,
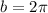
Thus,
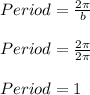
Thus period is 1