Answer:
The probability of number who disapprove of smoking pot daily is from 7 to 9 is 0.6293.
The probability of number who disapprove of smoking pot daily is at most 5 is 0.038601
The probability of number who disapprove of smoking pot daily is is not less than 8 is 0.723655.
Explanation:
The number of seniors that disapprove smoking pot daily X follows binomial distribution with n=12 and p=0.7 because
1. The opinion of seniors are independent.
2. There are two possible outcome approve or disapprove.
3. The probability of seniors disapproves smoking pot daily is constant for each trail i.e. p=0.7.
4. The opinion is asked from 12 senior i.e. fixed number of trails.
The probability of the number of seniors that disapprove smoking pot daily can be computed as
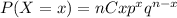
Here, n=12, p=0.7 and q=0.3.
P(number who disapprove of smoking pot daily is from 7 to 9)=P(7≤X≤9)=?
P(7≤X≤9)=P(X=7)+P(X=8)+P(X=9)
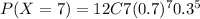 = 0.158496
= 0.158496
 = 0.231140
= 0.231140
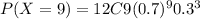 = 0.239700
= 0.239700
P(7≤X≤9)=0.158496+0.231140+0.239700
P(7≤X≤9)=0.6293
The probability of number who disapprove of smoking pot daily is from 7 to 9 is 0.6293.
P(number who disapprove of smoking pot daily is at most 5)=P(X≤5)=?
P(X≤5)=P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)+P(X=5)
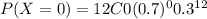 = 0.000001
= 0.000001
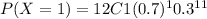 = 0.000015
= 0.000015
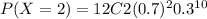 = 0.000191
= 0.000191
 = 0.001485
= 0.001485
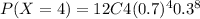 = 0.007798
= 0.007798
 = 0.029111
= 0.029111
P(X≤5)=0.000001+ 0.000015+ 0.000191+ 0.001485+ 0.007798+ 0.029111
P(X≤5)=0.038601
The probability of number who disapprove of smoking pot daily is at most 5 is 0.038601.
P(number who disapprove of smoking pot daily is not less than 8)=P(X≥8)=?
P(X≥8)=1- P(X<8)
P(X≥8)= 1-P(X≤7)
P(X≤7)=P(X≤5)+P(X=6)+P(X=7)
 = 0.079248
= 0.079248
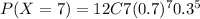 = 0.158496
= 0.158496
P(X≤7)=0.038601+ 0.079248+ 0.158496
P(X≤7)=0.276345
P(X≥8)=1-0.276345
P(X≥8)=0.723655
The probability of number who disapprove of smoking pot daily is is not less than 8 is 0.723655.