Question

The length of human pregnancies is approximately normally distributed with mean 266 days and standard deviation 16 days. Dr. Smith obtains a simple random sample of 10 of her patients and obtains the following results:

279 260 261 266 255 267 230 266 264 240
Construct a 90% confidence interval for the gestation period for all of Dr. Smith's patients. Interpret this interval. .

Answer 1

90% confidence interval for the gestation period for all of Dr. Smith's patients = [250.48 , 267.12] .

Explanation:

We are given that the length of human pregnancies is approximately normally distributed with Mean,
`\mu` = 266 days and standard deviation,
`\sigma` = 16 days.

Let suppose, Z =
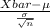`(Xbar - \mu)/((\sigma)/(√(n) ) )` follows N(0,1)

where,
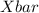`Xbar` = Sample mean =
`(279 +260 +261 +266+ 255+ 267+ 230+ 266+ 264+ 240)/(10)`

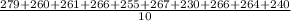
= 258.8

n = sample size = 10

So, the 90% confidence interval for
`\mu` is given by ;

P(-1.6449 < N(0,1) < 1.6449) = 0.90 {because at 10% level of significance z

table gives critical value of 1.6449}

P(-1.6449 <
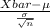`(Xbar - \mu)/((\sigma)/(√(n) ) )` < 1.6449) = 0.90

P(-1.6449*
`(\sigma)/(√(n) )` <
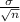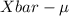`Xbar - \mu` < 1.6449*
`(\sigma)/(√(n) )` ) = 0.90

P(
`Xbar - 1.6449*(\sigma)/(√(n) )` <
`\mu` <
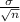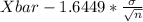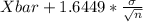`Xbar + 1.6449*(\sigma)/(√(n) )` ) = 0.90

So, 90% confidence interval for
`\mu` =
`[Xbar - 1.6449*(\sigma)/(√(n) ) , Xbar + 1.6449*(\sigma)/(√(n) )]`

=
`[258.8 - 1.6449*(16)/(√(10) ) , 258.8 + 1.6449*(16)/(√(10) )]`

= [250.48 , 267.12]

Since, 266 lies inside this interval so we conclude that the mean gestation period for all of Dr. Smith's patients is 266 days.

And this interval states that we have 90% confidence in the above statement.