Question

The density of ice is 917 kg/m3, and the density of sea water is 1025 kg/m3. A swimming polar bear climbs onto a piece of floating ice that has a volume of 6.22 m3. What is the weight of the heaviest bear that the ice can support without sinking completely beneath the water

Answer 1

671.76 kg or 6590 N

Step-by-step explanation:

So the buoyant force generated by the floating ice is equals to the mass of water displaced by the submerged ice. We also need to account for gravity of ice. The resulting additional mass that the ice sheet can support is the difference between the mass of water displaced by ice and the mass of ice submerged totally in water.

`m = m_w - m_i`

`m = V\rho_w - V\rho_i`

`m = V(\rho_w - \rho_i) = 6.22*(1025 - 917) = 671.76 kg`

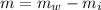
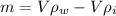
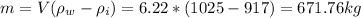
So the ice piece can support an additional 671.76 kg of bear, or 671.76 * 9.81 = 6590 N