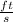Answer:
The velocity the air will enter the room through an opening is 20.9
Step-by-step explanation:
We have to consider 2 points
Point 1 = Being away from the laboratory door
Point 2 = Gab between the floor and the laboratory door
Using the Bernoulli equation
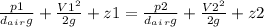
Assuming
p1 = patm
p2 = patm + plab
patm will be cancel and both points will be at the ground level
![0 = (plab)/(d_a_i_r g) + (V2^(2) )/(2g)\\ (V2^(2) )/(2g) = \sqrt[]{(-2plab)/(d_a_i_r) }](https://img.qammunity.org/2021/formulas/engineering/college/hb68gd5ws3pcne9cbtx23p1nj3evfcuauc.png)
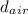 = - у H2O * hH2O
= - у H2O * hH2O
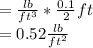
Substituting the results
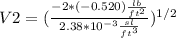
V2 = 20.9