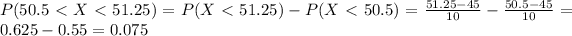Question

A statistics professor plans classes so carefully that the lengths of her classes are uniformly distributed between 45.045.0 and 55.055.0 minutes. Find the probability that a given class period runs between 50.550.5 and 51.2551.25 minutes.

Answer 1

`P(50.5 < X< 51.25)= P(X<51.25)-P(X<50.5) = (51.25-45)/(10)- (50.5-45)/(10)= 0.625-0.55=0.075`

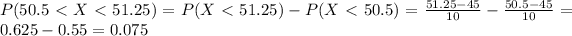
Explanation:

For this case we define X as our random variable representing the lenghts of her classes in minutes.

We know that the distribution for X is uniform and is given by:

`X \sim Unif (a=45.0, b=55.0)`

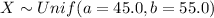
The density function is given by:

`f(x) = (1)/(55-45)= (1)/(10), 45 \leq X \leq 55`

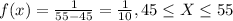
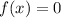`f(x)=0` for other case

The cumulative distirbution function is given by:

`F(x) = (x-45)/(55-45)= (x-45)/(10) , 45 \leq x \leq 55`

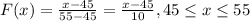
And we want to find this probability:

`P(50.5 < X< 51.25)`

We can find this probability using the cumulative distribution function and we got:

`P(50.5 < X< 51.25)= P(X<51.25)-P(X<50.5) = (51.25-45)/(10)- (50.5-45)/(10)= 0.625-0.55=0.075`