Question

asked May 9, 2021 171k views

1 Answer

Hituptony · Answer 1 · 2021-05-12T18:32:14+0000

Answer:

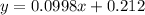
y=0.0998 x +0.212

For this case the slope means that for every increase of 1 unit in the Revenues we will have an increase of approximately 0.0998 in the net income.

We assume that Net Income (Y) and the Revenues represent (X)

See explanation below.

Explanation:

For this case w ehave the following data:

Year 1998 1999 2000 2001 2002 2003 2004 2005

Net Income 1.55 1.95 1.98 1.64 0.89 1.47 2.28 2.6

Revenues 12.42 13.26 14.24 14.87 15.41 17.14 19.07 20.46

We assume that Net Income (Y) and the Revenues represent (X)

For this case we need to calculate the slope with the following formula:

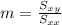
m=(S_(xy))/(S_(xx))

Where:

$S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)$

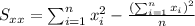
$S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)$

So we can find the sums like this:

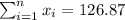
$\sum_(i=1)^n x_i =126.87$

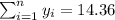
$\sum_(i=1)^n y_i =14.36$

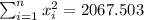
$\sum_(i=1)^n x^2_i =2067.503$

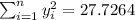
$\sum_(i=1)^n y^2_i =27.7264$

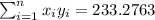
$\sum_(i=1)^n x_i y_i =233.2763$

With these we can find the sums:

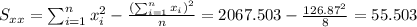
$S_(xx)=\sum_(i=1)^n x^2_i -((\sum_(i=1)^n x_i)^2)/(n)=2067.503-(126.87^2)/(8)=55.503$

$S_(xy)=\sum_(i=1)^n x_i y_i -((\sum_(i=1)^n x_i)(\sum_(i=1)^n y_i))/(n)=233.2763-(126.87*14.36)/(8)=5.544$

And the slope would be:

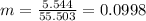
m=(5.544)/(55.503)=0.0998

Nowe we can find the means for x and y like this:

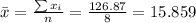
$\bar x= (\sum x_i)/(n)=(126.87)/(8)=15.859$

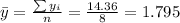
$\bar y= (\sum y_i)/(n)=(14.36)/(8)=1.795$

And we can find the intercept using this:

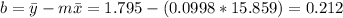
$b=\bar y -m \bar x=1.795-(0.0998*15.859)=0.212$

So the line would be given by:

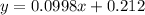
y=0.0998 x +0.212

For this case the slope means that for every increase of 1 unit in the Revenues we will have an increase of approximately 0.0998 in the net income.

Please log in or register to add a comment.