Question

A specimen of aluminum having a rectangular cross section 9.6 mm × 12.4 mm (0.3780 in. × 0.4882 in.) is pulled in tension with 35000 N (7868 lbf) force, producing only elastic deformation. The elastic modulus for aluminum is 69 GPa (or 10 × 106 psi). Calculate the resulting strain.

Answer 1

0.00426

Step-by-step explanation:

Young's modulus is given by the following expression,

`Y=(Stress)/(Strain) =(F/A)/(\Delta l/l)`

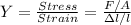
where,

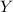`Y` = Young's modulus

`F` = force applied on the material

`A` = cross-sectional area

`l` = length of the material

`\Delta l` = elongation due to stress applied

For our problem, we need to find the strain of the aluminum specimen,

`Strain=(Stress)/(Y) =(F/A)/(Y)=(7868/(0.3780*0.4882))/(10*10^6) =0.00426`

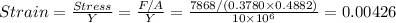
Strain is a ratio and hence a dimensionless quantity, so even if calculate using the values in S.I. units, we shall get the same value.