Answer:
BD = 30
Explanation:
AC is the perpendicular bisector of chord BD
The radius of the circle = AC = 8 + 9 = 17, thus
AD = 17
Let M be the point on BD where AC bisects it.
Using Pythagoras' identity in right triangle AMD
The square on the hypotenuse (AD) is equal to the sum of the squares on the other 2 sides, that is
MD² + 8² = 17² , that is
MD² + 64 = 289 ( subtract 64 from both sides )
MD² = 225 ( take the square root of both sides )
MD =
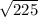 = 15
= 15
Thus BD = 2MD = 2 × 15 = 30