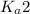Question

Phosphoric acid is a triprotic acid ( K a1 = 6.9 × 10 − 3 Ka1=6.9×10−3, K a2 = 6.2 × 10 − 8 Ka2=6.2×10−8, and K a3 = 4.8 × 10 − 13 Ka3=4.8×10−13). To find the pH of a buffer composed of H 2 PO − 4 ( aq ) H2PO4−(aq) and HPO 2 − 4 ( aq ) HPO42−(aq) , which p K a Ka value should be used in the Henderson–Hasselbalch equation?

Answer 1

Answer: To calculate the pH of the buffer composed of
`H_2PO_4^-\text{ and }HPO_4^(-2)`, we use the
`K_a2`

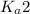
Step-by-step explanation:

Phosphoric acid is a triprotic acid and it will undergo three dissociation reaction each having their respective dissociation constants.

The chemical equation for the first dissociation reaction follows:

`H_3PO_4\rightleftharpoons H_2PO_4^-+H^+;K_a1=6.9* 10^(-3)`

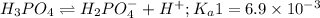
The chemical equation for the second dissociation reaction follows:

`H_2PO_4^-\rightleftharpoons HPO_4^(2-)+H^+;K_a2=6.2* 10^(-8)`

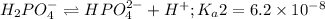
The chemical equation for the third dissociation reaction follows:

`HPO_4^(2-)\rightleftharpoons PO_4^(3-)+H^+;K_a3=4.8* 10^(-13)`

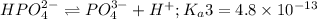
To form a buffer composed of
`H_2PO_4^-\text{ and }HPO_4^(-2)`, we use the
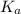`K_a` of second dissociation process

To calculate the
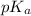`pK_a`, we use the equation:

`pK_a=-\log (K_a)\\\\pK_a=-\log(6.2* 10^(-8))\\\\pK_a=7.21`

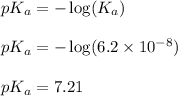
To calculate the pH of buffer, we use the equation given by Henderson Hasselbalch:

`pH=pK_a2+\log(\frac{[\text{conjugate base}]}{[\text{weak acid}]})`

`pH=pK_a2+\log(([HPO_4^(2-)])/([H_2PO_4^-]))`

We are given:

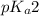`pK_a2` = negative logarithm of second acid dissociation constant of phosphoric acid = 7.21

`[HPO_4^(2-)]` = concentration of conjugate base

`[H_2PO_4^(-)]` = concentration of weak acid

Hence, to calculate the pH of the buffer composed of
`H_2PO_4^-\text{ and }HPO_4^(-2)`, we use the
`K_a2`