Question

Question #1: The visible part of the EM spectrum ranges from about 390 nanometers to about 720 nanometers. A nanometer (nm) is 10-9 meters or 1 billionth of a meter. The bluest light we see in a rainbow has a wavelength of about 400 nm; the reddest light we see in that rainbow has a wavelength of about 720 nm. Which color light (blue or red) is the highest in energy? Explain briefly

Answer 1

The blue light has the highest energy.

Step-by-step explanation:

Body that is hot enough emits light as consequence of its temperature. For example, an iron bar in contact with fire will start to change colors as the temperature increases until it gets to a blue color. That its know as Wien's displacement law, which establishes that the peak of emission for the spectrum will be displaced to shorter wavelengths as the temperature increases.

The same scenario described above can be found in the star, a star with higher temperature will have a blue color and one with lower temperature will have a red color.

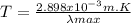`T = (2.898x10^(-3) m. K)/(\lambda max)` (1)

The energy of each wavelength can be determined by means of the following equation:

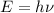`E = h\\u` (2)

but
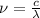`\\u = (c)/(\lambda)`, therefore:

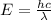`E = (hc)/(\lambda)` (3)

Where h is the planck's constant and
`\\u` is the frequency.

Notice that it is necessary to express the frequency in units of meters for a better representation of the energy.

`\\u_(blue) = 400nm . (1x10^(-9)m)/(1nm)` ⇒
`4x10^(-7)m`

`\\u_(red) = 720nm . (1x10^(-9)m)/(1nm)` ⇒
`7.2x10^(-7)m`

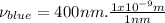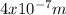
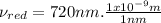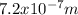
Case for the bluest light:

`E = ((6.626x10^(-34)J.s)(3x10^(8)m/s))/(4x10^(-7)m)`

`E = 4.96x10^(-19)J`

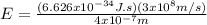
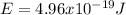
Case for the reddest light:

`E = ((6.626x10^(-34)J.s)(3x10^(8)m/s))/(7.2x10^(-7)m)`

`E = 2.76x10^(-19)J`

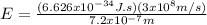
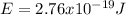
Equation 3 show that if the wavelength is lower the energy will be greater (inversely proportional).

Hence, according with the result and what was explained above, the blue light has the highest energy.