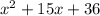Question

Refer to the rectangle below. The length of the rectangle is x + 12. The width of the rectangle is x + 3.

Please determine the area of the rectangle.

Answer 1

`x^2+15x+36`

Explanation:

The complete question is shown in the attachment.

The length of the rectangle is x + 12. The width of the rectangle is x + 3.

Recall that area of a rectangle is
`Length * Width`

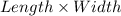
In terms of x, the area is
`(x+12)(x+3)`

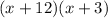
Recall the distributive property of real numbers:
`(a+b)(c+d)=a(c+d)+b(c+d)`

We apply this property to get:

`(x+12)(x+3)=x(x+3)+12(x+3)`

We expand again to get:

`(x+12)(x+3)=x^2+3x+12x+36`

We now simplify to obtain:

`(x+12)(x+3)=x^2+15x+36`

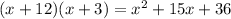
The area of the rectangle is
`x^2+15x+36`