Question

Triangle X Y Z is shown. Angle X Z Y is 63 degrees. The length of X Z is 2.7 and the length of X Y is 2.8. Law of sines: StartFraction sine (uppercase A) Over a EndFraction = StartFraction sine (uppercase B) Over b EndFraction = StartFraction sine (uppercase C) Over c EndFraction Which is the approximate measure of angle Y? Use the law of sines to find the answer. 52° 59° 64° 67°

Answer 1

The approximate measure of angle Y is 59° ⇒ 2nd answer

Explanation:

The formula of the sine law of a triangle is
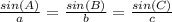`(sin(A))/(a)=(sin(B))/(b)=(sin(C))/(c)` , where

• a is the side opposite the angle A
• b is the side opposite to angle B
• c is the side opposite to angle C

In Δ XYZ

∵ The side YZ is opposite to ∠X

∵ The side XZ is opposite to ∠Y

∵ The side XY is opposite to ∠Z

- Write the sine formula

∴
`(sin(X))/(YZ)=(sin(Y))/(XZ)=(sin(Z))/(XY)`

∵ m∠XZY 63°

∵ The length of XZ = 2.7 units

∵ The length of XY = 2.8

- Substitute them in the sine formula

∴
`(sin(63))/(2.8)=(sin(Y))/(2.7)`

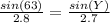
- By using cross multiplication

∴ 2.8 × sin(Y) = 2.7 × sin(63)

- Divide both sides by 2.8

∴ sin(Y) = 0.85918486

- Use the inverse of sine (
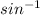`sin^(-1)`) to find y

∴ m∠Y =
`sin^(-1)(0.85918486)`

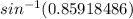
∴ m∠Y ≅ 59°

The approximate measure of angle Y is 59°

Answer 2

59°

Explanation:

For the triangle XYZ the sine theorem states that

`(XZ)/(\sin Y)=(XY)/(\sin Z)`

Since

`m\angle Z=63^(\circ)\\ \\XY=2.8\\ \\XZ=2.7,`

you have

`(2.7)/(\sin Y)=(2.8)/(\sin 63^(\circ))\\ \\2.8\sin Y=2.7\sin 63^(\circ)\\ \\\sin Y=(2.7\sin 63^(\circ))/(2.8)\\ \\\sin Y\approx 0.86\\ \\m\angle Y\approx 59^(\circ)`