The value of x is 15.56.
Solution:
Tangent and Secant theorem:
If one secant and one tangent are drawn to a circle from one exterior point, then the square of the length of the tangent is equal to the product of the external secant segment and the total length of the secant.
BE = 22 BD = x, CD = x
BC = x + x = 2x
By the tangent and secant theorem,


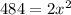
Divide by 2 on both sides of the equation, we get
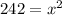
Take square root on both side of the equation.
x = 15.56
Hence the value of x is 15.56.