Question:
2x^2 + 5x + 3
What are the factors of the polynomial?
(2x+3)(x+1)
(2x-3)(x-1)
(3x+2)(x+1)
(3x-2)(x-1)
Answer:
Option A
The factors are:
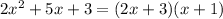
Solution:
Given that, the quadratic equation is:
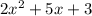
We have to find the factors of polynomial
Find the factors:
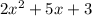
Split 5x as 2x and 3x
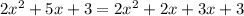
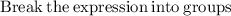
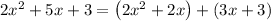
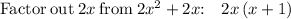
Thus we get,
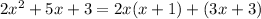
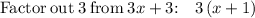
Thus we get,
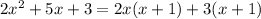
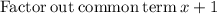
Thus we get,
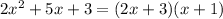
Thus the factors are found for given polynomial