Answer:
(a)

(b)
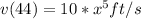
(c)

Explanation:

(a) when t = 44sec

s(44) ≅
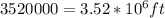
(b) How fast the hammer is traveling i.e. the speed of the hammer.
To find speed, we differentiate the distance s(t) with respect to time, t
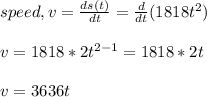
at t = 44sec,
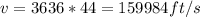
 ≅
≅
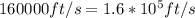
(c) The hammer's acceleration can be obtained by differentiating the speed v(t) with respect to time, t

There's no need to substitute t = 44sec because the acceleration is independent of time.