Question

It is known that every person has a 46% chance of making an impulse purchase at a specific grocery store. If 10 customers are randomly selected, to what is the probability that exactly 3 people make an impulse purchase at that grocery store

Answer 1

0.1563 is the required probability.

Explanation:

We are given the following information:

We treat chance of making an impulse purchase as a success.

P(chance of making an impulse purchase) = 46% = 0.46

Then the number of people make an impulse purchase follows a binomial distribution, since each trial in independent with two possible outcome and equal probability of success.

Formula:

`P(X=x) = \binom{n}{x}.p^x.(1-p)^(n-x)`

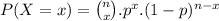
where n is the total number of observations, x is the number of success, p is the probability of success.

Now, we are given n = 10 and x = 3

We have to evaluate:

`P(x =3)\\= \binom{10}{3}(0.46)^3(1-0.46)^7\\= 0.1563`

0.1563 is the probability that exactly 3 people make an impulse purchase at that grocery store.