1) Yes
2) 66,000 miles
Explanation:
1)
The graph is missing, so you can find it in attachment.
Two variables y,x are said to be in a proportional relationship with each other when there exist a relationship in the form:
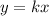
where
k is called "constant of proportionality"
In other words, two variables are in a proportional relationship if, when one of the two variable increases, the other one increases by the same proportion.
In this problem, the two variables represented are distance (y-axis) and time (x-axis); from the graph, we see that their relationship is represented by a straight line, which is in the form
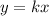 ; therefore, the two variables are in a proportional relationship.
; therefore, the two variables are in a proportional relationship.
2)
We can find the constant of proportionality by re-arranging the equation:
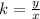
And by taking the values of y and x at a certain point along the graph.
For instance, by taking
x = 4 h
d = 48,000 mi
We find

which means that the probe travels 12,000 miles per hour.
Therefore, we can now find the distance travelled by the probe when
x = 5.5 h
We find:
