 ↔ zero product property and
↔ zero product property and
 ↔ square root property.
↔ square root property.
Solution:
Given expressions are
 and
and
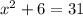 .
.
To find which techniques is most appropriate to solve each equation.
Equation 1:

Zero product property states that if AB = 0 then A = 0 or B = 0.
In the equation is
 , zero product property is used to solve the equation.
, zero product property is used to solve the equation.
(x + 3) = 0 (or) (x + 2) = 0
x = –3 (or) x = –2
Equation 2:
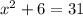
Subtract 6 from both sides of the equation.
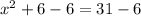
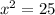
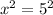
Take square root on both sides of the equation.
x = 5
Square root property is used to solve the equation.
Hence
 ↔ zero product property and
↔ zero product property and
 ↔ square root property.
↔ square root property.