Question

The balance of Micah's checking account is $648. Micah needs at least $800 in the account to cover his expenses. Write and solve an inequality that tells how much money Micah needs to deposit. Explain why there are infinite solutions to the inequality. plz hurry

Answer 1

The amount of money that Micah needs to deposit must be greater than or equal to $152

Explanation:

Let

x ----> amount of money that Micah needs to deposit

Remember that the word "at least" means "greater than o equal to"

we know that

The amount in the balance of Micah's checking account plus the amount that Micah will be deposit must be greater or equal to $800

so

The linear inequality that represent this situation is equal to

`648+x\geq 800`

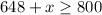
solve for x

subtract 648 both sides

`x\geq 800-648`

`x\geq\$152`

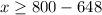
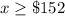
The amount of money that Micah needs to deposit must be greater than or equal to $152

There are infinite solutions to the inequality, because the solution is the interval [152,∞)