Answer:
53.73 factor
Step-by-step explanation:
Given that:
The activation energy (
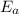 ) = 274 kJ/mol.
) = 274 kJ/mol.
T₁ = 255°C = (255+273) = 528 K
T₂ = 291° C = (291 + 273) = 564 K
Rate Constant (R) = 8.314 × 10⁻³ kJ k⁻¹ mol⁻¹
We are tasked to determine the factor at which the rate of the reaction increase as the temperature rises from 255°C to 291° C; In order to do that;
We can apply the use of Arrhenius Equation, which is given by:
㏑
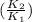 =
=
![(E_a)/(R) [(1)/(T_1)-(1)/(T_2)]](https://img.qammunity.org/2021/formulas/chemistry/college/62vtubh0ltcjjhu7jrxjxzcsvutw2uobyt.png)
㏑
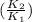 =
=
![(273kJ/mol)/(8.314*10^(-3)kJK^(-1)) [(1)/(528)-(1)/(564)]](https://img.qammunity.org/2021/formulas/chemistry/college/jwi3mmqivgs5tdo8ga2t6w37kmzhz669mj.png)
㏑
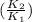 =
=
![(273kJ/mol)/(8.314*10^(-3)kJK^(-1)) [(36k)/((528K)(564K))]](https://img.qammunity.org/2021/formulas/chemistry/college/8a1exzvnjbvirk7wepbjjgh2zzww8zxsnz.png)
㏑
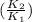 = 3.984
= 3.984
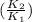 =
=
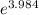
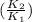 = 53.73
= 53.73
K₂ = 53.73 K₁
∴ As the temperature rises from 255°C to 291° C, the rate of reaction increases by 53.73 factor