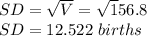Answer:
Mean = 160 births
Variance = 156.8 births
Standard deviation = 12.522 births
Explanation:
The mean number of births resulting in twins is given by the sample size (n=8000 births) multiplied by the probability of twins in any birth (p=2%).
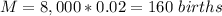
In a binomial distribution like this one, the variance is given by:
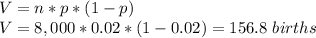
The standard deviation is simply the square root of the variance: