Question

Two automobiles leave the same city simultaneously and both head towards another city. The speed of one is 10 km/hour greater than the speed of the other, and this is why the first automobile arrives at the destination 1 hour before the other. Find the speed of both automobiles knowing that the distance between the two cities is 560 km.

Answer 1

5091 Km/hr and 505 km/hr

Explanation:

Speed = Distance / Time

Let the speed of first automobile be 'x' and that of the second be 'y'

Since speed of one is 10 times greater than the other. therefore;

⇒ x = 10 y

also let time for faster automobile be 'T' and time for slower auto mobile be 't'

Since first arrive one hour earlier than second, therefore;

⇒ t = T + 1

⇒ For first automobile;
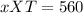`x X T = 560` ; substituting for 'x' and 'T'. Therefore;

⇒
`10y (t+1) = 560`

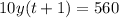
⇒ For Second automobile;
`y X t = 560`

⇒
`y = (560)/(t)`

⇒
`10((560)/(t))(t + 1) = 560`

⇒ 5600 +
`(5600)/(t)` = 560

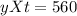
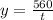
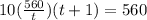
⇒ 560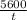0 - 560 = -
`(5600)/(t)`

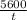
⇒ t = 1.11 hr

also ; T = 1.11 - 1 = 0.11 hr

Speed of 1st auto = 560/0.11 = 5091 km /hr

Speed of 2nd auto = 560/1.11 = 505 km/hr