Question

Let f(x)=a(2)^x. This exponential function is intersected twice by the line g(x)=x+b. One intersection is at point P(-2,2). Find the values of a and b. The other intersection occurs at point Q(r,s), where r and s are both integers. Find the values of r and s. Show algerbraically that r is a solution to the equation f(x)=g(x).

Answer 1

See below

Explanation:

To find the values of a and b, we use the intersection point P.

Since the graph of f is intersected by P=(-2,2), f(-2)=2, that is, a(2)^(-2)=2. Then a=2(2)²=8.

Since the graph of g is intersected by P=(-2,2), g(-2)=2, that is, -2+b=2. Then b=2+2=4.

Hence a=8, b=4.

To find the other point of intersection Q, we need to find a number x such that f(x)=g(x), that is, 8(2)^(x)=x+4. Rewrite this equation as follows:

`f(x)=8(2^x)=2^3(2^x)=2^(3+x)=g(x)=x+4`

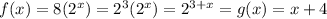
It is not easy to solve this equation analitically. Instead, you can apply a quantitative method. First, the left hand side is an exponential function, so it is always positive. Then the solution will be a number in which the right side (x+4) is positive, that is, x > -4. The solution is an integer, then the possible values are x=-3,-2,-1,0,1,2,...

Now, the RHS must be a power of two, so the possible integers are x=-3,-2,0,4,12,28,... However, the LHS grows very quickly, while the LHS grows slowly. Then, it is only necessary to test small integer values (we already know that x=-2 is a solution).

If we test with x=-1, we get 2²=4=3, then x=-1 is not a solution. Any x>-1 will not be a solution, because f increases much faster than g, and then they won't intersect. So our possibilities reduce to x=-3,-2. Taking x=-3, we get f(-3)=2⁰=1=-3+4=g(-3). Thus, (-3,0) is the other point of intersection Q. (r=-3, s=0).