Question

employees in an office wear eyeglasses. 23 have single-wision correction, and 25 wear bifocals. If two employees are selected at random from this group, the probability that both of them wear bifocals? What is the probability that both have single-vision correction? Round your answers to four decimal places. and 25 wear bifocals. If two employees are selected at random from this group, what is both employees wear bifocals )-ta2607 both employees have single-vision correction

Answer 1

26.60% probability that both of them wear bifocals.

22.43% probability that both have single-vision correction.

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

In this problem, the order of the employees is not important. For example, John and Elisa, or Elisa and John are the same outcomes.

This is why we use the combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

Total outcomes:

23+25 = 48 employees

Two selected. So

`T = C_(48,2) = (48!)/(2!(48-2)!) = 1128`

What is the probability that both of them wear bifocals?

25 wear bifocals.

Two selected. So

`D = C_(25,2) = (25!)/(2!(25-2)!) = 300`

`P = (D)/(T) = (300)/(1128) = 0.266`

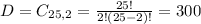
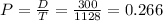
26.60% probability that both of them wear bifocals.

What is the probability that both have single-vision correction?

23 have single vision correction.

Two selected. So

`D = C_(23,2) = (23!)/(2!(23-2)!) = 253`

`P = (D)/(T) = (253)/(1128) = 0.2243`

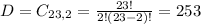
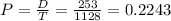
22.43% probability that both have single-vision correction.