Question

The following data give the prices of seven textbooks randomly selected from a university bookstore.

A. $91
B. $176
C. $108
D. $115
E. $56
F. $157
G. $144

a. Find the mean for these data. Calculate the deviations of the data values from the mean. Is the sum of these deviations zero?
Mean = $ Deviation from the mean for $176 = $ Sum of these deviations = $

b. Calculate the range, variance, and standard deviation. [Round your answers to 2 decimal places.] Range = $ Variance =

Answer 1

a) Mean = $121

Sum of deviations = $0

b) Standard deviation = 41.19

Variance = 1696.67

Range = $120

Explanation:

We are given the following data:

$91 , $176 , $108 , $115 , $56 , $157 , $144

a) Mean and sum of deviations

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(847)/(7) = 121`

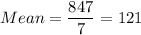
Sum of deviations =

-30 + 55 - 13 - 6 - 65 + 36 + 23 = 0

The sum of deviations is zero dollars.

b) range, variance, and standard deviation

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}}`

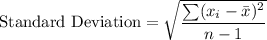
where
`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

Sum of square of differences =

900 + 3025 + 169 + 36 + 4225 + 1296 + 529 = 10180

`\sigma = \sqrt{(10180)/(6)} = 41.19\\\\\sigma^2 = 1696.67`

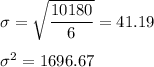
Sorted data: 56, 91, 108, 115, 144, 157, 176

Range = Maximum - Minimum

Range = 176 - 56 = 120