Question

Water flows at speed of 5.9 m/s through a horizontal pipe of diameter 3.1 cm . The gauge pressure P1 of the water in the pipe is 1.5 atm . A short segment of the pipe is constricted to a smaller diameter of 2.1 cm. What is the gauge pressure of the water flowing through the constricted segment?

Answer 1

The pressure will be 36169[Pa]

Step-by-step explanation:

We can solve this problem using the Bernoulli principle, so we have to identify the initial data of the problem.

`v_(1) = 5.9[m/s]\\d_(1) = 3.1[cm] = 0.031[m]\\ P_(1)=1.5[atm]= 1.5[atm]*(101.325kPa)/(1atm) = 151.98[kPa]`

`d_(2)=2.1[cm]=0.021[m]`

Now we can state the Bernoulli equation

`P_(1)+(1)/(2)*dens_(1)*v_(1)^(2)+dens_(1)*g*h_(1)= P_(2)+(1)/(2)*dens_(2)*v_(2)^(2)+dens_(2)*g*h_(2)`

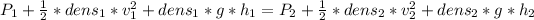
As the fluid inside the pipe does not undergo considerable height changes the last term on the right and left side of the equation can be canceled.

Therefore:

`P_(1)+(1)/(2)*dens_(1)*v_(1)^(2)= P_(2)+(1)/(2)*dens_(2)*v_(2)^(2)`

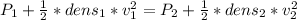
The density is the same both at the inlet and at the outlet of the pipe.

`dens_(1)= dens_(2)=dens=1000[kg/m^(3)]`

In bernoulli's equation we have to find the value of Velocity V2, so we can then clear the pressure value P2. To be able to find V2 we have to find the value of the flow that circulates inside the pipeline and then find V2

`Q=v_(1)*((\pi )/(4)*0.031^(2) ) \\Q = 5.9*((\pi )/(4)*0.031^(2) )\\Q=4.45*10^(-3)[m^(3)/s]`

Now:

`v_(2) =(Q*4)/(\pi *0.021^(2) ) \\v_(2)=(0.004453*4)/(\pi *0.021^(2) )\\v_(2)=12.85[m/s]`

Now we can find pressure P2

`P_(2) =P_(1)+(1)/(2) *dens*v_(1)^(2) -(1)/(2) *dens*v_(2)^(2)\\P_(2) =101325+(1)/(2) *1000*5.9^(2) -(1)/(2) *1000*12.85^(2)\\P_(2)=36168.75[Pa]`