Question

A parallel-plate capacitor is charged by connecting it across the terminals of a battery. If the battery remains connected and the separation between the plates is increased, what will happen to the charge on the capacitor and the voltage across it?

Answer 1

The voltage ( or potential difference) V increases while the charge Q decreases.

Step-by-step explanation:

The capacitance C of a capacitor is defined as the measure to which the capacitor can store charges. For a parallel-plate capacitor it is given by the following relationship;

`C=(\epsilon_o\epsilon_rA)/(d)............(1)`

where A is the surface area of the plates, d is their distance of separation,
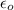`\epsilon_o` is the permittivity of free space and
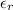`\epsilon_r` is relative permittivity.

Also, the capacitance of a capacitor can be expressed in the form of equation (2)

`C=(Q)/(V)...................(2)\\`

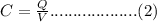
where Q is the charge stored and V is the potential difference.

By combining (1) and (2) and making d the subject of formula, we obtain the following;

`d=(\epsilon_o\epsilon_rAV)/(Q)............(3)`

By observing (3), it is seen that the distance d of separation between the plates is directly proportional to the potential difference V and inversely proportional to the charge stored Q. This implies that an increase in the distance d of separation will bring about an increase the the voltage or potential difference V and a decrease in the charge Q.