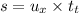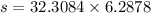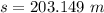Answer:
Step-by-step explanation:
Given:
- initial velocity of projectile,
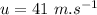
- angle of projection above horizontal,
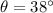
height of the initial projection point above the ground,
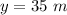
Vertical component of the velocity:
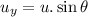
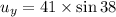
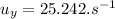
The time taken in course of going up:
(at top the final velocity will be zero)
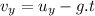
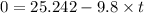

In course of going up the maximum height reached form the initial point:
(at top height the final velocity is zero. )
using eq. of motion,
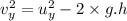
where:
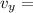 final vertical velocity while going up.=0
final vertical velocity while going up.=0
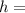 maximum height
maximum height
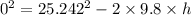
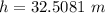
Now the total height to be descended:


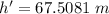
Now the time taken to fall the gross height in course of falling from the top:
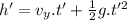
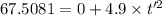
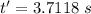
Now the total time the projectile spends in the air:
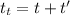
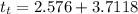
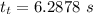
Now the horizontal component of the initial velocity:
(it remains constant throughout the motion)

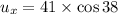
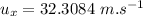
Therefore the horizontal distance covered in the total time;