Question

Given that H2 (g) + F2 (g) ⟶ 2HF (g) ΔH ∘ rxn = − 546.6 kJ 2H2 (g) + O2 (g) ⟶ 2H2O (l) ΔH∘rxn = − 571.6 kJ calculate the value of ΔH∘rxn for 2F2 (g) + 2H2O (l) ⟶ 4HF (g) + O2 (g)

Answer 1

Answer : The value of
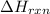`\Delta H_(rxn)` for the reaction is, -521.6 kJ

Explanation :

According to Hess’s law of constant heat summation, the heat absorbed or evolved in a given chemical equation is the same whether the process occurs in one step or several steps.

According to this law, the chemical equation can be treated as ordinary algebraic expression and can be added or subtracted to yield the required equation. That means the enthalpy change of the overall reaction is the sum of the enthalpy changes of the intermediate reactions.

The given main reaction is,

`2F_2(g)+2H_2O(l)\rightarrow 4HF(g)+O_2(g)`
`\Delta H_(rxn)=?`

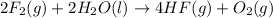
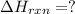
The intermediate balanced chemical reaction will be,

(1)
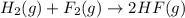
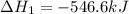
`H_2(g)+F_2(g)\rightarrow 2HF(g)`
`\Delta H_1=-546.6kJ`

(2)
`2H_2(g)+O_2(g)\rightarrow 2H_2O(l)`
`\Delta H_2=-571.6kJ`

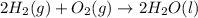
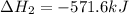
Now we are multiplying reaction 1 by 2 and reversing reaction 2 and then adding all the equations, we get :

(1)
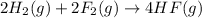
`2H_2(g)+2F_2(g)\rightarrow 4HF(g)`
`\Delta H_1=2* (-546.6kJ)=-1093.2kJ`

(2)
`2H_2O(l)\rightarrow 2H_2(g)+O_2(g)`
`\Delta H_2=571.6kJ`

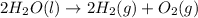
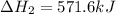
The expression for enthalpy of change will be,

`\Delta H=\Delta H_1+\Delta H_2`

`\Delta H=(-1093.2kJ)+(571.6kJ)`

`\Delta H=-521.6kJ`

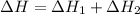
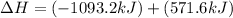
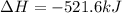
Thus, the value of
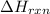`\Delta H_(rxn)` for the reaction is, -521.6 kJ