Question

In a large sample of customer accounts, a utility company determined that the average number of days between when a bill was sent out and when the payment was made is 32 with a standard deviation of 7 days. Assume the data to be approximately bell-shaped.. Between what two values will approximately 68% of the numbers of days be?. Estimate the percentage of customer accounts for which the number of days is between 18 and 46.. Estimate the percentage of customer accounts for which the number of days is between 11 and 53.

Answer 1

Estimate the percentage of bills for number 39 when a bill was sent and when payment was made Answer:

Step-by-step explanation: yes

Answer 2

• Question 1: between 25 and 39 days

• Question 2: about 95%

• Question 3: about 99.7%

Step-by-step explanation:

Question 1. Between what two values will approximately 68% of the numbers of days be?.

You can answer based on the 68-95-99.7% rule. As per this rule, about 68% of the data of a normal distribution (bell shaped) are within one standard deviation of the mean.

Here the mean is 32 day and the standard deviation is 7 day. Then 68% are in the interval 32 days ± 7 days.

That is:

• 32 days + 7 days = 39 days

• 32 days - 7 days = 25 days

Consequently, approximately 68% of the numbers of days will be between 25 and 39 days.

Question 2. Estimate the percentage of customer accounts for which the number of days is between 18 and 46.

First must determine the Z-scores both both values X = 18 and X = 46

The formula is:

`Z-score = (X-mean)/(standard\text{ }deviation)`

• For X = 18

`Z-score=(18-32)/7=-2`

• For X = 46

`Z-score=(46-32)/7=2`

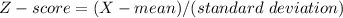
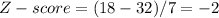
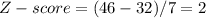
Hence, you want to estimate the percentage of customers accounts for which the the number of days is within 2 standard deviations of the mean.

As per the 68-95-99.7 rule about 95% of the data are within 2 standard deviations of the mean. You can calculate it also from a standard normal distribution table, finding the area to the left of Z-score = - 2 and subtracting the area to the right of Z-score equal to 2: That is: 0.9772 - 0.0228 = 0.9484 = 95.44% ≈ 95%.

Question 3. Estimate the percentage of customer accounts for which the number of days is between 11 and 53.

Again, determine the Z-scores for the two values, X = 11 and X = 53.

• For X = 11:

`Z-score=(11-32)/7=-3`

• For X = 53:

`Z-score=(53-32)/7=3`

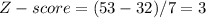
Hence, you want to estimate the probability of the number of days s between - 3 and 3 standard deviations.

Such probability is about 99.7%, according to the 68-95-99.7 rule.

If you use a standard distritution table you will find that the area to the right of the Z-score of -3 is 0.99865, thus the probability of the Z-score be to the right of 3 is 1 - 0.99865 = 0.00135.

And the probability in between -3 and 3 standard deviations is 0.99865 - 0.00135 = 0.9973 = 99.73% ≈ 99.7%.