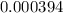Question

In five-card poker, a straight consists of five cards with adjacent denominations (e.g., 9 of clubs, 10 of hearts, jack of hearts, queen of spades, and king of clubs). Assuming that aces can be high or low, if you are dealt a five-card hand, what is the probability that it will be a straight with high card 9? (Round your answer to six decimal places.)

Answer 1

`0.000394`

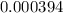
Explanation:

First we will find the probability of selecting five cards out of pack of cards

Probability of selecting five cards is equal to

`^(52)C_5`

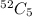
On expanding we get

`(52!)/(47! * 5!) \\`

`(52 * 51 * 50 * 49 * 48 * 47!)/(47 ! * 5*4*3*2*1) \\= 2598960`

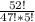
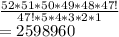
straight high card
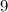`9` means five cards with values lesser than
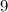`9` but adjacent to it are

`9, 8, 7, 6, 5`

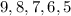
there are four card for each number

Hence, probability of choosing five cards is equal to

`4*4*4*4*4\\= 1024`

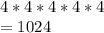
Probability of getting a straight with high card 9 is equal to

`(1024)/(2598960)`

`0.000394`