Question

A muon has a rest mass energy of 105.7 MeV, and it decays into an electron and a massless particle. If all the lost mass is converted into the electron’s kinetic energy, what is the electron’s velocity?

Answer 1

The electron’s velocity is 0.9999 c m/s.

Step-by-step explanation:

Given that,

Rest mass energy of muon = 105.7 MeV

We know the rest mass of electron = 0.511 Mev

We need to calculate the value of γ

Using formula of energy

`K_(rel)=(\gamma-1)mc^2`

`(K_(rel))/(mc^2)=\gamma-1`

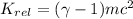
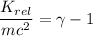
Put the value into the formula

`\gamma=(105.7)/(0.511)+1`

`\gamma=208`

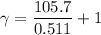
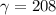
We need to calculate the electron’s velocity

Using formula of velocity

`\gamma=\frac{1}{\sqrt{1-((v)/(c))^2}}`

`\gamma^2=(1)/(1-(v^2)/(c^2))`

`\gamma^2-\gamma^2*(v^2)/(c^2)=1`

`v^2=(1-\gamma^2)/(-\gamma^2)* c^2`

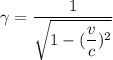
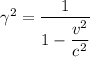
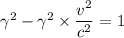
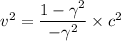
Put the value into the formula

`v^2=(1-(208)^2)/(-208^2)* c^2`

`v=c\sqrt{(1-(208)^2)/(-208^2)}`

`v=0.9999 c\ m/s`

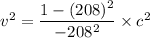
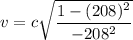
Hence, The electron’s velocity is 0.9999 c m/s.