Question

2019 Indianapolis 500 winner Simon Pagenaud holds his hand out of his Indy car window while driving through still air with standard atmospheric conditions. a) For safety, the pit lane speed limit is 60 mph. At that speed, what is the maximum pressure on his hand. Governing Equation: Assumptions: Solution: b) Back on the race track, what is the maximum pressure on his hand when driving at 225 mph? c) If the speed of sound at track level is 761 mph, what is the Mach number at a maximum speed of 240 mph? d) Is it reasonable to assume the flow is incompressible?

Answer 1

Step-by-step explanation:

Part (a):

Using the equation of pressure gradient for velocity, along the streamline:

`P_1 = P \;+\; (1)/(2)\;\rho\;V^2 \;+\; \rho_(air)gz\\`

where,

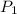`P_1` = Required pressure

`P` = Atmospheric pressure

`V` = Velocity of the Flow

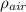`\rho_(air)` = Density of air at 1500m above sea level

Assuming the flow as incompressible, above equation becomes

`P_1 = P \;+\; (1)/(2)\;\rho\;V^2`

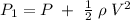
Substituting values for pressure and density, we get

`P_1 \;= \;14.7(lb)/(in^2) \;+\; (1)/(2)[(0.002376(sl)/(ft^3)).\;(60\;mph)^2]\\\\(Standard\; values\; at\; atmospheric\; conditions)\\\\P_1\;=\;14.7(lb)/(in^2).(144\;in^2)/(ft^2) \;+\; (1)/(2)[(0.002376(sl)/(ft^3)).\;(60\;mph\;.\;(1.4667\; (ft)/(s))/(mph))^2]\\\\P_1\;=\; 2126\;\; lb/ft^2`

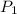`P_1` = 14.76 psi

Part (b):

Just replace the value of velocity with 225 mph in part (a). All other values and equations will remain the same.

`P_2 \;= \;14.7(lb)/(in^2) \;+\; (1)/(2)[(0.002376(sl)/(ft^3)).\;(225\;mph)^2]\\\\(Standard\; values\; at\; atmospheric\; conditions)\\\\P_2\;=\;14.7(lb)/(in^2).(144\;in^2)/(ft^2) \;+\; (1)/(2)[(0.002376(sl)/(ft^3)).\;(225\;mph\;.\;(1.4667\; (ft)/(s))/(mph))^2]\\\\P_2\;=\; 2246.17\;\; lb/ft^2`

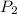`P_2` = 15.59 psi

Part (c):

It is given that the speed of sound is 761 mph, which is equal to 1 mach. Therefore, to convert the maximum car speed of 240 mph, we simply divide it by the speed of sound.

Mach Speed =
`(240)/(761)`

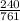
Mach Speed = 0.315 Mach

Part (d):

The difference between compressible and incompressible flow is that, in compressible flow, the density of the fluid varies with pressure, while in incompressible flow, the density remains constant. Compressible flows are usually high speed flows with Mach numbers greater than 0.3 (for example air flow over an aircraft's wing). Therefore, a fluid moving around or below Mach 0.3 is typically considered incompressible, even if it is a gas.

As for our scenario, the mach number for maximum possible speed was only around Mach 0.3, we can assume this as an incompressible flow

Answer 2

See attachment below

Step-by-step explanation: